

Next: About this document ...
Up: No Title
Previous: 2. Your Responsibility
The design team has found the following ``test'' case has all the
properties of the more difficult problem faced by the client. The bitmap
or matlab ``image'' is
in the form of this matlab script.
This
script, when saved as disks.m and run under matlab will generate
3 overlapping solid-colored disks, as can be seen by clicking here.
The image is an
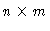 matrix of
positive integers. The entries in the matrix are then
mapped onto a colormap, thus producing a colored image of the data.
This data is thus a matrix W=wi,j of positive integers. There is a
one-to-one map between the integers and an array of colors. You should
carefully study disks.m before proceeding.
The tasks are:
matrix of
positive integers. The entries in the matrix are then
mapped onto a colormap, thus producing a colored image of the data.
This data is thus a matrix W=wi,j of positive integers. There is a
one-to-one map between the integers and an array of colors. You should
carefully study disks.m before proceeding.
The tasks are:
- 1.
- Design and implement an efficient
algorithm that is geometry independent that detects the edges of the
disks, i.e. you should be able to resolve
three rings representing the perimeter of the disks.
The code edgdet.m should produce a bitmap
(matlab image) which when displayed shows the edges of the three disks,
as seen by clicking here.
Wherever an edge has been detected use a
threshold value (a positive integer) to force the colormap to display
the image as shown in the figure. It
will take as input the raw data W and produce a matrix C=ci,j
of type image of the same size as W, which when displayed, will show
the edges of the disks.
The script disks.m will generate the matrix W, saved as disk_d.mat. This will be the ``raw data''. Note:
be very careful on how you use the matlab clear
command in this assignment, since you are running several scripts, one
after the other one.
- 2.
- Design and implement one or both of the edge-processing
algorithms:
- (a)
- (P2) DIFFUSION SMOOTHER:
produce an algorithm and a code, named difedg.m, that implements the following: we'll use diffusion to
produce a new matrix S, of the same size as C, which yields an
image of a smoother version of the edges. The matrices S and C
can be restructured in your code as
vectors of size
![$[(n \times m)] \times 1$](img3.gif) .
Call these new
vectors
.
Call these new
vectors 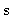 and
and 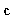 ,
respectively.
The smoothing is effected by the
general operator
,
respectively.
The smoothing is effected by the
general operator
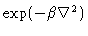 ,
which when discretized,
produces a discrete operator (matrix) M.
Here,
,
which when discretized,
produces a discrete operator (matrix) M.
Here, 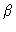 is a real number and is the
smoothing parameter. The Laplacian operator
is a real number and is the
smoothing parameter. The Laplacian operator
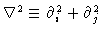 .
The smoothed, edge-detected data
.
The smoothed, edge-detected data 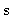 is given by the mapping
is given by the mapping
|
(1) |
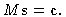 |
|
|
The notes for 475B
will prove useful here: look at the material on the
``matrix exponential'' and on the ``5-point formula for the Laplacian''
for what follows:
- i.
- Prove that under proper conditions
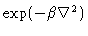 is an invertible operator. What are those
conditions?
is an invertible operator. What are those
conditions?
- ii.
- Analitically, prove that (1) will effect a smoother version
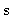 of
of 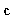 ,
provided
,
provided 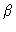 is chosen properly.
is chosen properly.
- iii.
- Expand
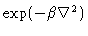 into a finite series. Explain
mathematically what effect the operator has on the data when 1, 2,
3, and k>3 terms are retained, as a function of
into a finite series. Explain
mathematically what effect the operator has on the data when 1, 2,
3, and k>3 terms are retained, as a function of 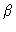 .
.
- iv.
- Using only two terms in the series expansion, write down a
discretization of the smoothing operator. Assume that n=m.
- v.
- Design and implement an efficient algorithm that implements the
discretization of the two term expansion case. To get the desired
efficiency will require that it be iterative. Show that the scheme
converges for any size of input matrix.
- (b)
- (P3) ADVECTION-DIFFUSION SMOOTHER: this approach gives you two
parameters to control the outcome of the filter: one of them is the
diffusion smoothing produced by the Laplacian. The other one is a
sharpening of the image by the action of an advective term
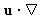 .
These are competing effects, when
.
These are competing effects, when
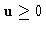 .
The idea is to solve
.
The idea is to solve
![$[\partial_n + {\bf u}\cdot
\nabla - \beta \nabla^2] {\bf c} = 0$](img12.gif) ,
integrating in
``time'' n until it reaches an equilibrium configuration. Here,
,
integrating in
``time'' n until it reaches an equilibrium configuration. Here,
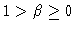 .
If the
system reaches equilibrium, then
.
If the
system reaches equilibrium, then
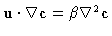 .
This equilibrium state of
.
This equilibrium state of 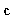 is the desired
is the desired 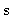 .
Why use time n? Because a
finite-difference discretization, with
.
Why use time n? Because a
finite-difference discretization, with
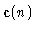 yields the
semi-discrete problem
yields the
semi-discrete problem
i.e. a time evolution problem with time step of 1. The initial data is
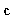 ,
the edge-detected data. The final solution, for nsufficiently large, would hopefully be
,
the edge-detected data. The final solution, for nsufficiently large, would hopefully be 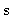 ,
or some reasonable
approximation of it. Recasting this problem as an evolution problem will
immediately suggest an iterative scheme for the resulting linear
algebraic problem once the above equation is discretized in i,j. The
only remaining question is to find a good choice of value for the input
parameter
,
or some reasonable
approximation of it. Recasting this problem as an evolution problem will
immediately suggest an iterative scheme for the resulting linear
algebraic problem once the above equation is discretized in i,j. The
only remaining question is to find a good choice of value for the input
parameter 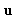 .
One possibility is to use
.
One possibility is to use
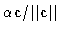 ,
where
,
where
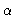 is a fine tuning parameter.
is a fine tuning parameter.
- i.
- Design and implement an iterative scheme that implements the
advection diffusion scheme. It is rather straightforward if you designed the P2 code
properly. TAKE A LOOK AT HW6 FROM 475B FOR SPARSE MATRIX
CONSTRUCTION IN MATLAB
- ii.
- Discuss how you would go about choosing the parameters
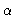 and
and 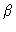 ,
so that the iterative scheme will converge.
,
so that the iterative scheme will converge.
- iii.
- Discuss how you would choose the parameters with the range
estimated above, that will lead you to useful graphical results.
- iv.
- Make an estimate of the computational cost of the algorithm and
compare it to the P2 algorithm.


Next: About this document ...
Up: No Title
Previous: 2. Your Responsibility
JuanRestrepo
1999-11-13
![]() matrix of
positive integers. The entries in the matrix are then
mapped onto a colormap, thus producing a colored image of the data.
This data is thus a matrix W=wi,j of positive integers. There is a
one-to-one map between the integers and an array of colors. You should
carefully study disks.m before proceeding.
The tasks are:
matrix of
positive integers. The entries in the matrix are then
mapped onto a colormap, thus producing a colored image of the data.
This data is thus a matrix W=wi,j of positive integers. There is a
one-to-one map between the integers and an array of colors. You should
carefully study disks.m before proceeding.
The tasks are: